有限自动机、正则表达式与词法分析

这篇文章适合学过「形式语言与自动机」这门课的同学阅读。为了可读性，本文中使用的均为 Python 代码。

「有限自动机」与「正则表达式」 #

首先，我们来探讨一下有限自动机和正则表达式。

有限自动机是一个规则很死板的状态机器，负责处理一个字符串，然后判断这个字符串是不是符合一个规则，有限自动机会返回一个结果：这个字符串是否匹配的一个布尔值。

正则表达式是一种规则，它与 有限自动机 等价。值得注意的是，我们这里提到的正则表达式并非实际编程应用的正则表达式（如Perl / Python / JavaScript 等中的，下称「现代正则表达式」），而是符合「正则文法」的表达式，其中只允许以下内容：

1. 连接（Concatenation）： 把两个子表达式接起来，例如 ab 表示字符串 "a" 后面跟 "b"。

2. 并（Union / Alternation）： 使用 | 表示“或者”，比如 a|b 表示 "a" 或 "b"。

3. 闭包（Kleene star）： 使用 * 表示重复 0 次或多次，比如 a* 表示 "", "a", "aa", "aaa", ...。

4. 加号（+）和问号（?）： 虽然不是基础构造，但它们是 * 的语法糖：

   • a+ 相当于 aa*
   • a? 相当于 a|ε（表示可有可无）

5. 字符类（[abc]）或单字符匹配： DFA 可以处理固定的字符选择，比如 [a-c]，其实相当于 a|b|c。

6. 空串 ε（epsilon）： 表示可以匹配“什么都没有”，在构造中经常用到。

我们能用这些简单的规则来构造出足以实现词法分析的复杂规则。词法分析（Lexical Analysis）是编程语言编译器的第一阶段，它的任务是把源代码中的一长串字符，切分成一个个有意义的「词」（token）。

下面来看一些例子：

token_spec = [
    ("NUMBER",     r"\d+"),             # 匹配整数
    ("IDENTIFIER", r"[a-zA-Z]+"),       # 匹配变量名（字母）
    ("PLUS",       r"\+"),              # 匹配加号
    ("WHITESPACE", r"\s+"),             # 匹配空格（跳过）
]

我们用现代正则表达式的语法描述了整数、变量名、加号、空格这四种「词」。接着编译器需要扫描源代码，用这几种正则表达式来匹配字符，输出一个词的列表。

「正则表达式」与「现代正则表达式」 #

「正则表达式」最初是由数学家 Stephen Kleene 提出的，这些语言可以由 有限自动机 识别。

然而，当正则表达式被引入到编程语言和实际工程应用中后，它的语法得到了极大的扩展。现代主流编程语言中使用的正则表达式引擎，已经加入了许多超出正则语言表达能力的功能，比如反向引用（backreference）、零宽断言（lookahead、lookbehind）以及条件语法等。这些扩展功能使得现代正则表达式能够处理比正则语言更复杂的文本结构。

当你在编程语言中编写了一个「现代正则表达式」时，编译器 / 解释器会做些什么呢？

1. 先解析这个表达式的语法。它会识别出像 \d 是数字，{3} 是重复次数，- 是字面字符等。
2. 接着，正则引擎会把这个正则「编译」成一个内部结构，它是一个自动机，但未必是「有限自动机」。正则表达式中如果使用了一些无法被有限自动机表达的语法，就会构造一个非有限自动机。
3. 当这个「自动机」构造好后，你可以用它来匹配任何字符串。在最简单的实现中，这个自动机会返回布尔值，关于匹配成功或否。更复杂的实现可能会支持分组捕获、回溯等高级功能。

因为我们了解了「现代正则表达式」的实现机制，所以就能解释为什么在实际应用中，使用正则表达式匹配字符串的效率往往远低于直接使用一些字符串函数。而且，对于需要反复使用的正则表达式，应当提前编译再重复使用，而不是每次都重复编译，例如在 Python 中：

import re

code = "a + 23 + b"

token_spec = [
    ("NUMBER",     r"\d+"),             # 匹配整数
    ("IDENTIFIER", r"[a-zA-Z]+"),       # 匹配变量名（字母）
    ("PLUS",       r"\+"),              # 匹配加号
    ("WHITESPACE", r"\s+"),             # 匹配空格（跳过）
]

pattern = re.compile("|".join(f"(?P<{name}>{regex})" for name, regex in token_spec))

# 一个简化的词法分析器
for match in pattern.finditer(code):
    kind = match.lastgroup
    value = match.group()
    if kind != "WHITESPACE":
        print(f"{kind}: {value}")

我们使用re.compile函数编译了正则表达式，这样之后的匹配过程中就可以复用这个自动机，而不是每次都重新编译。

有限自动机 #

讲了这么多正则表达式的内容，还没有讲什么是有限自动机呢！先给出一个简单的例子：

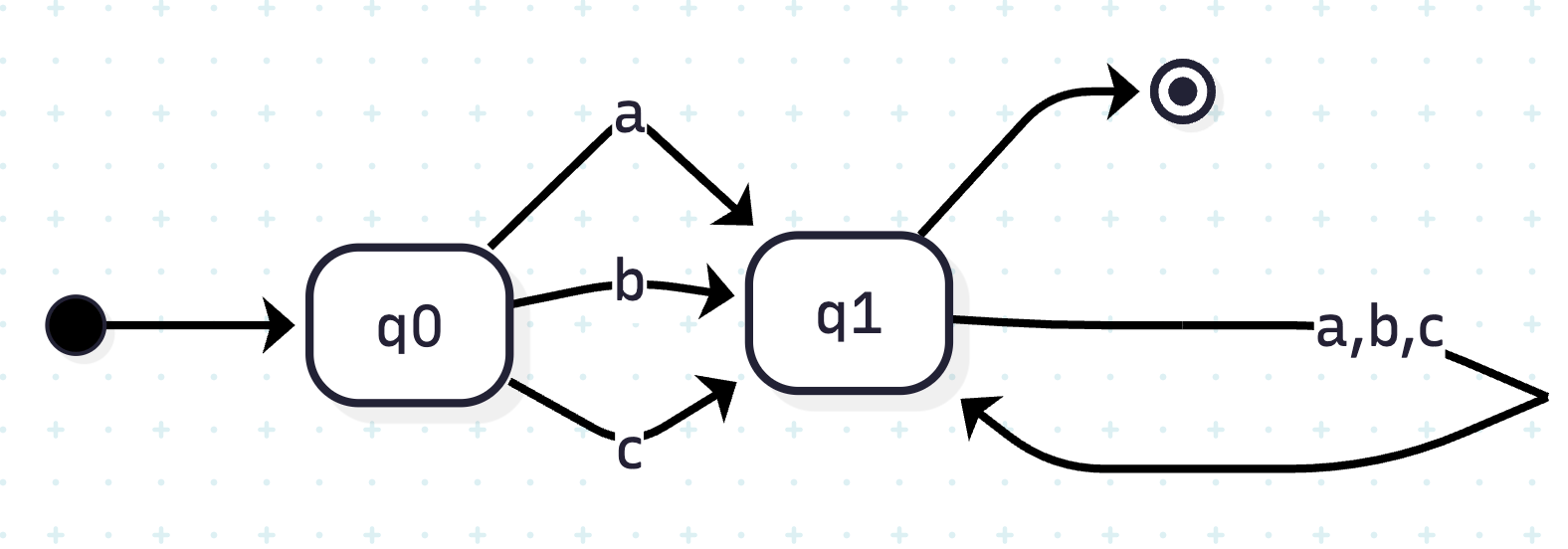
这个例子对应的正则表达式是(a|b|c)+，或者现代正则表达式中可以表示为[abc]+。

这种图叫「状态图」，定义了初始状态、状态转换和接受状态等。依次读入字符串，状态会随之变化（如果没有对应的转换则不变化，例如在这个例子中读到x时）。当所有字符都读入后，如果状态在接受状态上，则匹配成功，否则匹配失败。

有限自动机的匹配过程大致如下：

class DFA:
    def __init__(self):
        self.transitions = {
            'q0': {'a': 'q1', 'b': 'q1', 'c': 'q1'},
            'q1': {'a': 'q1', 'b': 'q1', 'c': 'q1'},
        }
        self.start_state = 'q0'
        self.accept_states = {'q1'}

    def match(self, input_string):
        current_state = self.start_state
        print(f"Start at state: {current_state}")
        # 遍历读入字符串中的字符
        for char in input_string:
            if char not in self.transitions[current_state]:
                # 出现了字母表之外的字符，直接拒绝
                return False
            # 从转移表中获取下一个状态，并更新当前状态
            next_state = self.transitions[current_state][char]
            current_state = next_state
        # 返回接受或拒绝的布尔值
        return current_state in self.accept_states

你可以在这个 网站 中实现任意正则表达式向有限自动机的转换，其源代码在 这里 。有限自动机还分为 NFA 和 DFA（如果你上过形式语言与自动机的课一定会被要求掌握两种自动机之间的相互转化），它们不在我们本文的重点中，所以这里就不展开了。